Common Mistakes in Solving Circle Equations and How to Master Center-Radius Form for SAT Mathematics

When solving problems involving circles, students often make common mistakes when interpreting and converting equations. Let’s break down how to avoid these mistakes and properly handle circle equations.

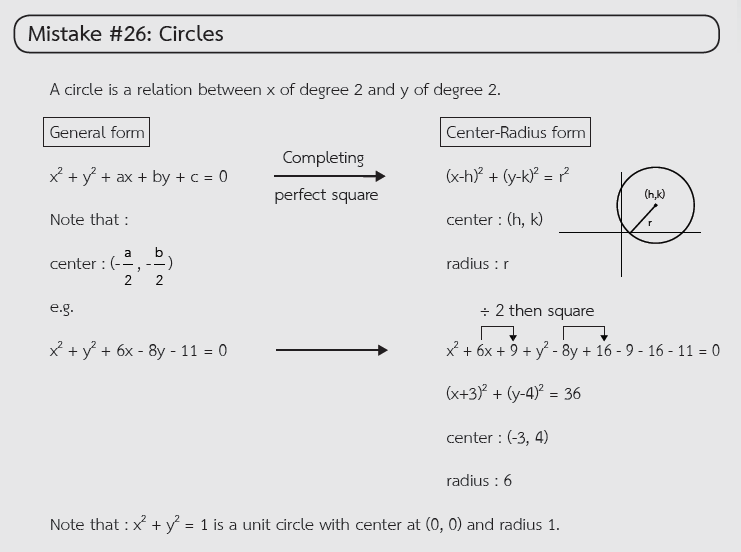
1. Understanding the General Form of a Circle Equation
   A circle is a relation between x and y, both of degree 2. The general form of a circle equation is written as x² + y² + ax + by + c = 0. In this form, the center of the circle is at (-a/2, -b/2) and the radius can be calculated once the equation is rewritten correctly. A common mistake is not correctly recognizing the center and radius from the general form.

2. Converting to Center-Radius Form
   The center-radius form of the equation is (x – h)² + (y – k)² = r², where (h, k) is the center and r is the radius. To convert the general form into this format, students often need to complete the square on both x and y terms. A typical mistake is skipping the completing the square process or making errors while solving for the center and radius.

3. Example of Completing the Square
   Let’s take the example x² + y² + 6x – 8y – 11 = 0. To convert this into center-radius form, first complete the square:
   x² + 6x → (x + 3)²
   y² – 8y → (y – 4)²
   After completing the square and simplifying, you get (x + 3)² + (y – 4)² = 36. The center is (-3, 4) and the radius is 6. A common mistake here is either not completing the square correctly or missing the step of factoring the equation properly.

4. Unit Circle
   It’s important to note that the equation x² + y² = 1 represents a unit circle, which has its center at (0, 0) and a radius of 1. Misunderstanding this equation can lead to errors in identifying the properties of the unit circle and its graph.

By understanding these common mistakes and knowing how to correctly complete the square and convert equations into center-radius form, you can accurately solve problems related to circles. Always make sure to carefully complete the square, recognize the center and radius, and apply these steps to solve circle equations with confidence.