เรื่องที่ออกบ่อยๆ ในเมทริกซ์ไม่พ้น 2 เรื่องนี้แน่ๆ
การหาค่าของเมทริกซ์อินเวอร์ส (Inverse Matrix)
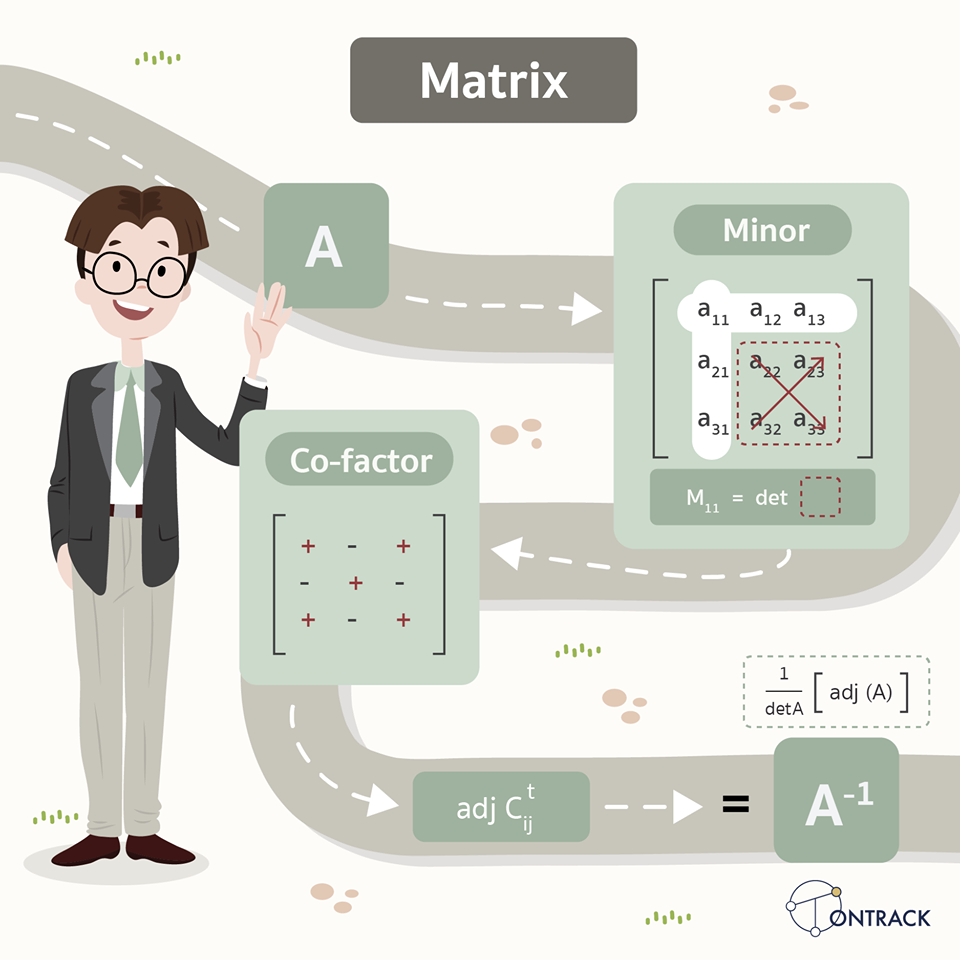
การหาค่าของเมทริกซ์อินเวอร์สเป็นขั้นตอนที่สำคัญในคณิตศาสตร์ที่เกี่ยวข้องกับเมทริกซ์ ซึ่งสามารถทำได้ด้วยขั้นตอนดังนี้:
- การหา Minor Minor คือการคำนวณที่ทำได้โดยการตัดแถวและตัดหลักที่ต้องการออกจากเมทริกซ์ จากนั้นคำนวณค่า determinant (det) ของเมทริกซ์ที่เหลืออยู่ ตัวอย่างเช่น หากต้องการคำนวณค่า Minor สำหรับตำแหน่ง 1,1 ในเมทริกซ์ 3×3 ให้ตัดแถวแรกและหลักแรกออกแล้วคำนวณ det ของเมทริกซ์ 2×2 ที่เหลือ
- การหา Co-factor Co-factor คือการคำนวณที่ได้จากการเอา Minor ของแต่ละตำแหน่งมา คูณด้วย -1 หรือ 1 ขึ้นอยู่กับตำแหน่งของมันในเมทริกซ์ สำหรับเมทริกซ์ 3×3 จะมีแค่ 4 ตัวที่ต้องคูณ -1
- การหา Adj Adj (Adjugate) ได้จากการทำ Transpose ของ Co-factor matrix นั่นคือ การสลับแถวและหลักของ Co-factor matrix
- การคำนวณ Inverse เมทริกซ์อินเวอร์ส (A⁻¹) สามารถหาได้โดยการคำนวณตามสูตรดังนี้: A⁻¹ = (1/det(A)) * adj(A)
การคำนวณเมทริกซ์อินเวอร์สนี้สำคัญในหลายๆ ด้านเช่น การแก้ระบบสมการเชิงเส้น, การหาค่าของเมทริกซ์ที่ใช้งานในการคำนวณต่างๆ
พร้อมจะฝึกเพิ่มเติมหรือยัง? อ่านสรุปจุดผิดทั้งหมดและฝึกทำโจทย์จากหนังสือของเรา!
