Common Mistakes in SAT Math Pythagorean Theorem

Examples of Common Mistakes in SAT Math – Pythagorean Theorem Tips from STUDYPLAN

Common Mistakes with the Pythagorean Theorem

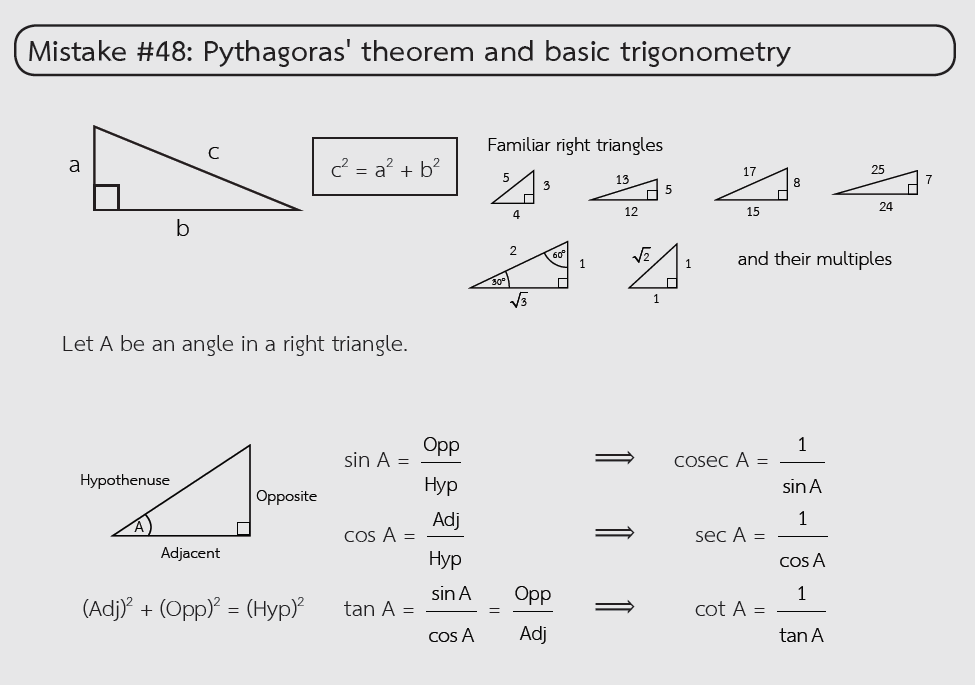
The Pythagorean Theorem, a fundamental concept in geometry, is essential for solving right triangle problems on the SAT Math section. While the formula c2 = a2 + b2 (where c is the hypotenuse and a and b are the legs) is simple, students often make several common mistakes when applying it. Here’s a breakdown of these errors and how to avoid them:

1. MISIDENTIFYING THE HYPOTENUSE

A frequent mistake is confusing the hypotenuse with one of the legs. Remember, the hypotenuse is always the longest side, opposite the right angle. When using the Pythagorean Theorem, ensure you’re correctly identifying which side is the hypotenuse.

2. INCORRECTLY USING TRIGONOMETRIC RATIOS

Trigonometric functions like sine, cosine, and tangent are often used in SAT Math problems, but students can mistakenly apply them without understanding their proper relationships in a right triangle. The sine of an angle is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side. These relationships are used to find missing sides or angles but should not replace the Pythagorean Theorem when solving for a side in a right triangle.

3. FAILING TO RECOGNIZE SPECIAL RIGHT TRIANGLES

Certain triangles, such as the 3-4-5 or 5-12-13 triangles, are commonly seen in SAT Math problems. Students may overlook these familiar patterns and attempt to apply the theorem in a more complicated manner. Always recognize when a right triangle follows a well-known pattern to save time.

4. FORGETTING TO APPLY THE THEOREM CORRECTLY IN WORD PROBLEMS

In word problems, it’s easy to misinterpret the question and forget to apply the Pythagorean Theorem correctly. Ensure you’re using the theorem only when the question involves a right triangle, and carefully assign the correct values to a, b, and c.

5. CONFUSING TRIGONOMETRIC FUNCTIONS WITH RECIPROCAL FUNCTIONS

Sometimes, students incorrectly swap trigonometric functions for their reciprocals. For instance, the cosecant is the reciprocal of sine, the secant is the reciprocal of cosine, and the cotangent is the reciprocal of tangent. These should only be used when explicitly required by the question and should not replace basic geometric principles like the Pythagorean Theorem.

CONCLUSION

The Pythagorean Theorem is a key tool in SAT Math, but to use it effectively, students must avoid common mistakes like misidentifying sides, misusing trigonometric ratios, and overlooking special triangles. Practice identifying the right triangles and applying the formula correctly to improve your SAT Math performance.